Electronic Supplement to
Moment Tensor Inversions of Icequakes on Gornergletscher, Switzerland
by F. Walter, J. F. Clinton, N. Deichmann, D. S. Dreger, S. E. Minson, and M. Funk
Background Info
Motivation for Study of Various Source Types
A large variety of seismic sources such as explosions, shear faults, tensile crack openings, as well as combinations thereof can be represented by a linear combination of elastic responses to force couples. The relative strengths of the individual force couples are given by a 2nd rank symmetric moment tensor (e. g. Aki and Richards, 1980). Thus, moment tensors contain information about underlying seismic source mechanisms and pose a rigorous characterization of seismic sources.
The inversion of broadband waveform data from seismograms to produce moment tensor source mechanisms is common to study seismic sources (see Jost and Hermann, 1989 for a review). An unconstrained full moment tensor inversion may suffer from numerical instabilities (Dufumier and Rivera, 1997). This problem is usually tackled by imposing mathematical constraints in the inversion scheme. A common example is the inversion of tectonic earthquakes, where the isotropic component of the moment tensor is forced to vanish, as the sources are usually expected to be double-couple. In this case, a large compensated linear vector dipole (CLVD) component usually indicates errors with the Green's Functions.
A nonzero isotropic component indicates that the source region undergoes a volumetric change during the seismic event. In order to interpret the volumetric change calculated from the isotropic moment correctly, the source geometry must be taken into account (Müller, 2001).
An explosion possesses a purely isotropic moment tensor. A shear fault, associated with tectonic earthquakes, gives rise to a purely deviatoric double couple moment tensor. The CLVD can also be completely described by a deviatoric moment tensor.
The CLVD source mechanism does not correspond to a specific observed physical process, but can be explained by more complicated mechanisms. Examples are shear faulting near discontinuities of elastic moduli, rapid polymorphic phase changes (Julian, et al., 1998) and tensile cracks accompanied by compensating implosions (Julian and Sipkin, 1985). The CLVD source has been used to describe volcanic events (e. g. Julian and Sipkin, 1985) and deep earthquakes (Knopoff and Randall, 1970).
An important example of a source represented by a combination of an isotropic and a deviatoric moment tensor is the tensile fracture, also referred to as the 'tensile crack' model. The deviatoric part is a pure CLVD and its strength relative to the isotropic component is dependent on the Poisson's ratio of the material constituting the source (see following section). In the present work we assume a Poisson's ratio of 0.36 which was found to yield good waveform fits and lies in the ranges of Poisson's ratios for ice as given in Turcotte and Larson (2002). For comparison, Minson et al. (2007) assume a Poisson solid with a Poisson's ratio of 0.25 for the source region of volcanic events. With the Poisson's ratio used in the present icequake study, the isotropic component of the tensile crack moment tensor is almost five times larger than the CLVD.
A linear combination of the double-couple and the tensile crack moment tensors (henceforth 'crack+DC') constitutes a model that is highly relevant to the present work. Recently, Minson et al. (2007) applied the crack+DC model to seismic and geodetic data of the 2000 Miyakejima volcanic earthquake swarm. The authors argue that this model is particularly applicable to seismic events induced by magma propagation. In the case of glacial seismicity we expect tensile fracturing, which represents a special case of the crack+DC model, to be a likely failure model. Under normal flow conditions the opening direction of pervasive crevasses is parallel to that of maximum tension, even in regions of simple shear such as near the glacier margin (Paterson, 1994). Representing a tensile fracture, a tensile crack model thus provides a plausible mechanism for crevasses opening. On the other hand, Roberts et al. (2000) observed fracturing on the surface of Icelandic glaciers that developed during glacial lake drainages and showed some indication of shear failure. This suggests that during rapidly changing dynamic or hydrological conditions, glacier ice may undergo shear failure. The crack+DC moment tensor poses a plausible model for both, crevasses opening and shear faulting caused by abnormal ice flow, as well as any superposition of the two processes.
Deviatoric and crack+DC moment tensors are used in constrained moment tensor inversions. Besides yielding numerical stability, constrained moment tensor inversions are a means of testing the applicability of a certain source mechanism. For instance, in the present work we will repeatedly test the hypothesis of a tensile crack source solution for icequakes by comparing the fit quality of the crack+DC inversion to that of the full moment tensor inversion. If the latter results in significantly higher fit qualities, the tensile crack moment tensor does not explain the observed seismograms, but if both equally well solve the problem, the simple, constrained mechanism is proposed.
Decomposition of Tensile Crack Moment Tensor
The moment density tensor of a tensile opening in the z-plane ('tensile crack' moment density tensor) mcrack is given by
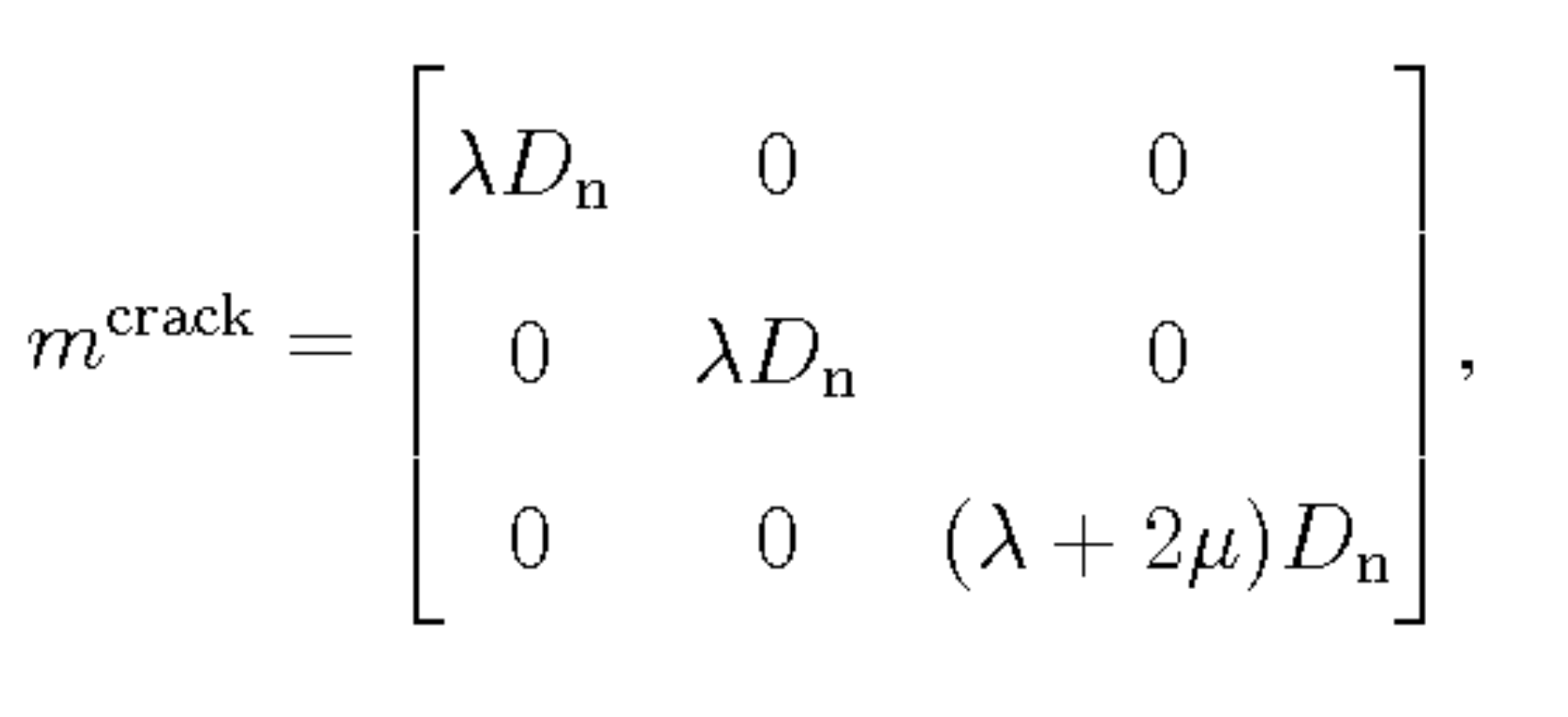 |
(1) |
where Dn is the fault normal slip and and λ and μ are the Lamé moduli (Aki and Richards, 2002, p. 51). To get the moment tensor Mcrack, the expression in Equation 1 has to be multiplied by the fault area S. Thus, using ν = 1/2 λ / (λ + μ) where ν is the Poisson's ratio, we obtain
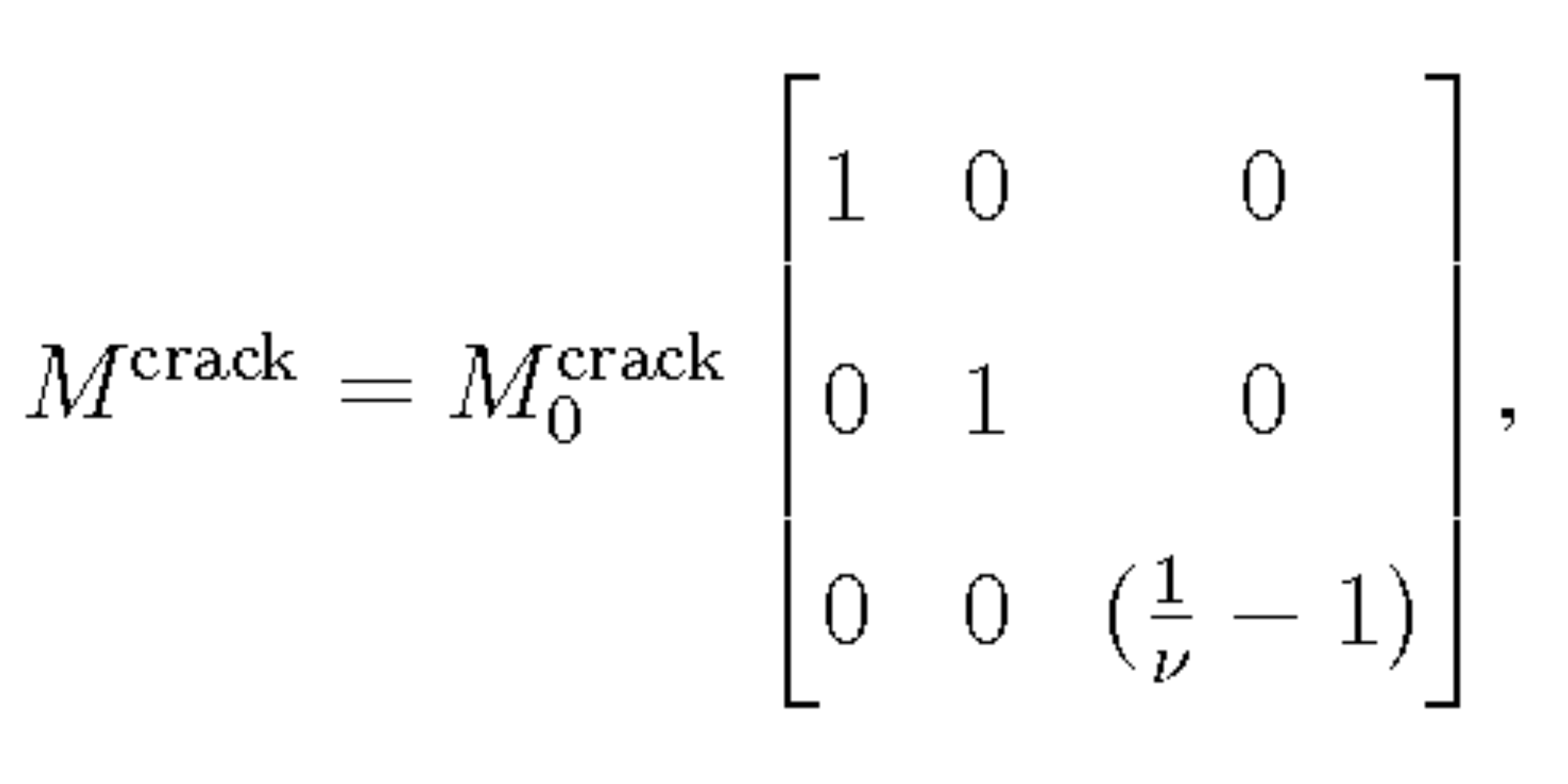 |
(2) |
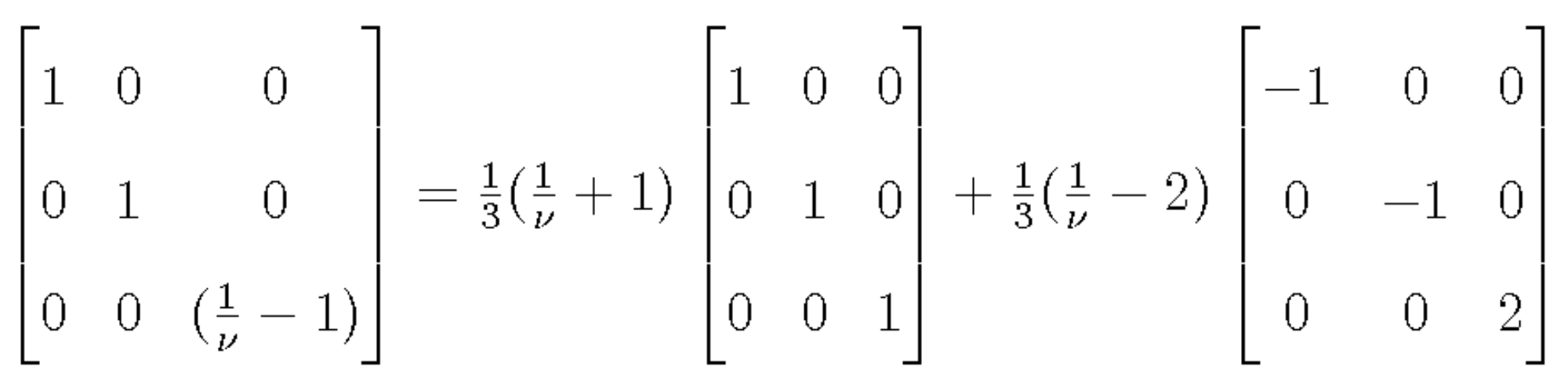 |
(3) |
Equation 3 shows that the moment tensor of a tensile crack in the z-direction is a linear combination of an isotropic moment tensor and a CLVD that has its major axis in the z-direction. The relative strength of the two depends on the Poisson's ratio of the material surrounding the source. For ν=0.36, the value used in this study, the isotropic component is almost 5 times bigger than the CLVD.
Decomposition of Tensile Crack Moment Tensor
The artificial scaling of the sampling frequency and the source-receiver distances affects the calculation of the scalar moment. To determine the scaling factor of the scalar moment corresponding to a scaling of distance and frequency by a factor of 1000, consider the following analytical expression for the scalar moment of a double-couple source (e. g. Boatwright, 1980):
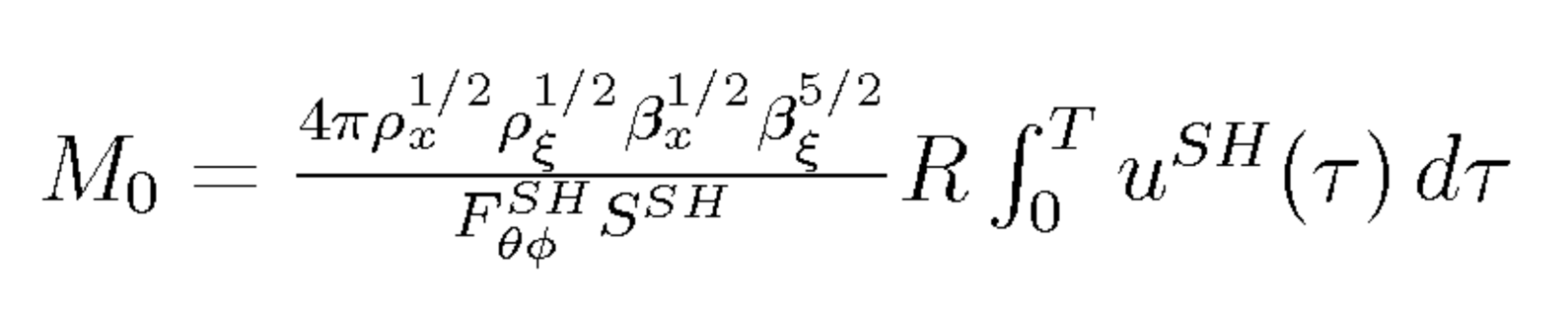 |
(4) |
Here, ρx and ρξ are the densities at the station and source, respectively. βx and βξ are the respective S-velocities. Fθ φSH is the radiation coefficient and SSH is the free-surface amplification; R is the hypocentral distance and uSH(t) is the ground displacement due to the SH-wave. The integration is performed over the duration of the S-wave T. The calculation in Equation 4 can also be applied to P or SV-waves. However, in these cases the free-surface amplification is affected by mode conversions, whereas in the case of SH-waves it is simply a factor of two. Scaling the sampling interval increases the value of the integral by a factor of 1000. Another factor of 1000 enters the expression via scaling of the source-receiver distance R. Therefore, the scalar moment is overestimated by a factor of 106. This was verified for each event with forward modelling of the waveforms using the reflectivity code. For a double-couple event, Equation 4 constitutes a second possibility for calculating the scalar moment using the unscaled signals. Although the result of the moment tensor inversion overestimates the scalar moment by 4, the fault plane geometry and the corresponding radiation coefficient Fθ φSH are unchanged as geometry is unaffected by the scaling. This can then be used together with SH displacement of the unscaled seismograms integrated in the time domain to obtain the scalar moment. Once the corrected scalar moment has been determined, we calculate the moment magnitude, Mw, via (Hanks and Kanamori, 1979)
 |
(5) |
Note that in this equation M0 is given in units of Nm.
Source-Type Plots
Following Hudson et al. (1989) we use source-type plots as a means to characterize the calculated moment tensors (Figure 1 in the electronic supplement). Source-type plots are a means to illustrate the source mechanism represented by a moment tensor using the two parameters k (near-horizontal lines) and T (near-vertical lines), which are calculated from the deviatoric eigenvalues and the isotropic moment Miso as follows:
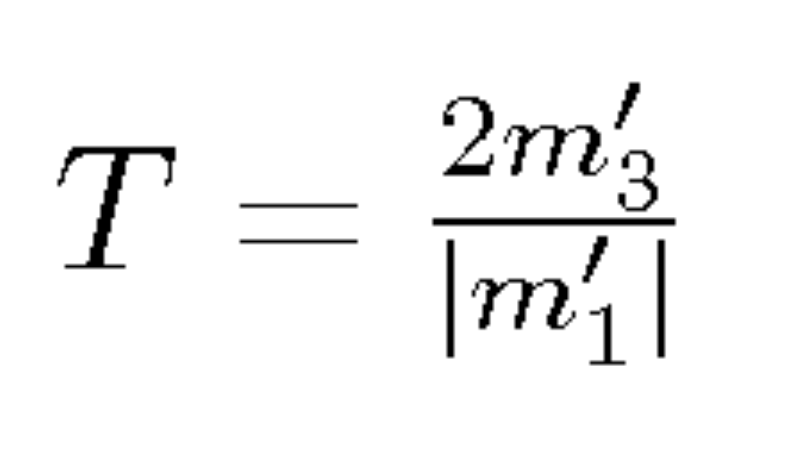 |
(6) |
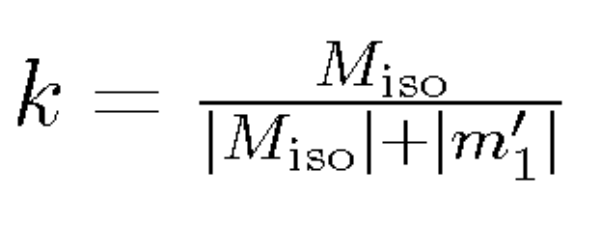 |
(7) |
The representation of a moment tensor using these parameters is independent of the geometry of the source, such as fault plane orientations. The parameter k characterizes the degree of isotropic component, with k=0 yielding a purely deviatoric and k=1 (k=-1) an explosion (implosion) moment tensor. Thus, any purely deviatoric source is plotted on the horizontal line k=0. The parameter T indicates how much the deviatoric moment tensor component differs from a pure double-couple source. (T,k)=(0,0) represents a pure double-couple, whereas (T,k)=(-1,0) and (T,k)=(1,0) are the parameters of a pure positive and negative CLVD, respectively. The moment tensors of a tensile crack source added to a double-couple source lie on a line connecting the positive and negative crack via the double-couple location, assuming that the tensile crack and double-couple fault planes coincide (Julian et al., 1998). The special feature of source-type plots is that a given area on the (T,k) grid is proportional to the probability that the T and k values of a moment tensor lie within this area, assuming no a priori constraints on any moment tensor element.
Bibliography
Aki, K. and Richards, P. G. (2002). Quantitative Seismology. University Science Books, Sausalito, California, second edition.
Boatwright, J. (1980). A spectral theory for circular seismic sources; simple estimates of source dimension, dynamic stress drop, and radiated seismic energy. Bulletin of the Seismological Society of America, 68:1117-1131.
Dufumier, H. and Rivera, L. (1997). On the resolution of the isotropic component in moment tensor inversion. Geophys. J. Int., 131(3):595-606.
Hanks, T. C. and Kanamori, H. (1979). A moment magnitude scale. Journal of Geophysical Research, 84(B5):2348-2350.
Hudson, J. A., Pearce, R. G., and Rogers, R. M. (1989). Source type plot for inversion of the moment tensor. Journal of Geophysical Research, 94:765-774.
Jost, M. L. and Herrmann, R. B. (1989). A Student's Guide to and Review of Moment Tensors. Seismological Research Letters, 60(2):37-57.
Julian, B. R., Miller, A. D., and Foulger, G. R. (1998). Non-double-couple earthquakes (theory). Reviews of Geophysics, 36(4):525-549.
Julian, B. R. and Sipkin, S. A. (1985). Earthquake processes in the Long Valley Caldera area, California. Journal of Geophysical Research, 90:11,155-11,169.
Knopoff, L. and Randall, M. J. (1970). The compensated linear vector dipole: A possible mechanism for deep earthquakes. Journal of Geophysical Research, 75:4957-4963.
Minson, S. E., Dreger, D. S., Bürgmann, R., Kanamori, H., and Larson, K. M. (2007). Seismically and geodetically determined nondouble-couple source mechanisms from the 2000 miyakejima volcanic earthquake swarm. Journal of Geophysical Research, 112.
Müller, G. (2001). Volume change of seismic sources from moment tensors. Bulletin of the Seismological Society of America, 91:880-884.
Paterson, W. S. B. (1994). The Physics of Glaciers. Pergamon, New York, third edition.
Roberts, M. J., Russell, A. J., Tweed, F. S., and Knudsen, O. (2000). Ice fracturing during jökulhlaups: implications for englacial floodwater routing and outlet development. Earth Surface Processes and Landforms, 25:1429-1446.
Turcotte, D. L. and Schubert, G. (2002). Geodynamics. Cambridge University Press, second edition.